04.01.13
Postulates of Boolean Algebra
As we know there are three logic gates to define various logics and on the basis of same Boolean Algebra have some basic postulates (fundamental laws) as follows:
1. OR relations (which is also known as logical addition, as it has four cases: 0+0=0, 0+1=1, 1+0=1, 1+1=1)
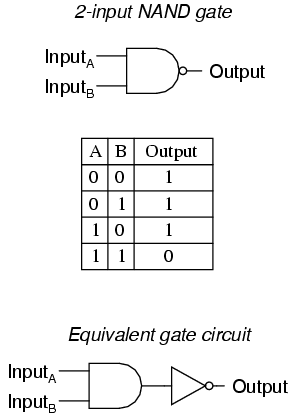
2. AND relations (which is also known as logical multiplication, as it has four cases: 0.0=0, 0.1=0, 1.0=0, 1.1=1)
3. NOT relations (which is also known as complement rule, as it has two cases: 0=1, 1=0)
Before we start, lets have a look on Principle of Duality in boolean expressions:
Principle of Duality means, that by making changes into the given boolean expression, another boolean expression can be derived. Following changes can be made to the given boolean expression:
0 + 0 = 0, will become, 1 . 1 = 1, after principle of duality is applied to it. And the boolean expression derived is known as DUAL OF ORIGINAL EXPRESSION. And if we see closely, 1 . 1 = 1, is also Postulate II of Boolean Algebra.
This tutorial is based on: "Computer Science - Seventh Edition" book by 'Sumita Arora' Pages: 659-660.
Postulates of Boolean Algebra
As we know there are three logic gates to define various logics and on the basis of same Boolean Algebra have some basic postulates (fundamental laws) as follows:
1. OR relations (which is also known as logical addition, as it has four cases: 0+0=0, 0+1=1, 1+0=1, 1+1=1)
2. AND relations (which is also known as logical multiplication, as it has four cases: 0.0=0, 0.1=0, 1.0=0, 1.1=1)
3. NOT relations (which is also known as complement rule, as it has two cases: 0=1, 1=0)
Before we start, lets have a look on Principle of Duality in boolean expressions:
Principle of Duality means, that by making changes into the given boolean expression, another boolean expression can be derived. Following changes can be made to the given boolean expression:
- Changing each OR with AND (+ with .) and its reverse (changing . with +)
- Replacing each 0 bit with 1 bit and its reverse, replacing 1 bit with 0 bit.
0 + 0 = 0, will become, 1 . 1 = 1, after principle of duality is applied to it. And the boolean expression derived is known as DUAL OF ORIGINAL EXPRESSION. And if we see closely, 1 . 1 = 1, is also Postulate II of Boolean Algebra.
This tutorial is based on: "Computer Science - Seventh Edition" book by 'Sumita Arora' Pages: 659-660.
Next topic: 07.01.13: Lecture 9: Theorems of Boolean Algebra












 is used between any two statements P and
Q to form a compound statement P
is used between any two statements P and
Q to form a compound statement P  is called the biconditional and may be
placed between any two statements to form a compound statement P
is called the biconditional and may be
placed between any two statements to form a compound statement P