#include<iostream>
using namespace std;
class tv
{
int channel,volume;
int on;
int get_channel()
{
channel=1;
return channel;
}
int get_vol()
{
volume=1;
return volume;
}
public:
tv()
{
channel=get_channel();
volume=get_vol();
cout<<"\n current channel is : "<<channel<<" and volume is : "<<volume;
}
void turn_on()
{
on=1;
}
void turn_off()
{
on=0;
}
void set_channel(int m)
{
channel=m;
cout<<"\n Current channel is"<<channel;
}
void set_volume (int n)
{
volume =n;
cout<<"\n current volume is"<<volume;
}
void channel_up()
{
channel+=1;
cout<<"\n current channel is"<<channel;
}
void channel_down()
{
channel-=1;
cout<<"\n current channel is"<<channel;
}
void vol_up()
{
volume+=1;
cout<<"\n current volume is"<<volume;
}
void vol_down()
{
volume-=1;
cout<<"\n current volume is"<<volume;
}
};
void main()
{
int x,y,z;
tv t1;
do
{
cout<<"do you want to make any changes (1/0)";
cin>>x;
if (x == 1)
{
cout<<"1. turn off \n 2.turn on \n 3. channel up \n 4. channel down \n 5.set channel \n 6.volume up \n 7.volume down \n 8.set volume \n";
cout<<"enter the number ";
cin>>y;
if (y==1)
{
t1.turn_off();
break;
}
switch (y)
{
case 2:
t1.turn_on();
break;
case 3:
t1.channel_up();
break;
case 4:
t1.channeldown();
break;
case 5:
{
cout<<"\n enter the channel no (1-120)";
cin>>z;
t1.set_channel(z);
}
break;
case 6:
t1.vol_up();
break;
case 7:
t1.vol_down();
break;
case 8:
{
cout<<"\n enter the volume level(1-7)";
cin>>z;
t1.set_volume(z);}
break;
}
}
}
while(x== 1);
cout<<"thank you";
}
using namespace std;
class tv
{
int channel,volume;
int on;
int get_channel()
{
channel=1;
return channel;
}
int get_vol()
{
volume=1;
return volume;
}
public:
tv()
{
channel=get_channel();
volume=get_vol();
cout<<"\n current channel is : "<<channel<<" and volume is : "<<volume;
}
void turn_on()
{
on=1;
}
void turn_off()
{
on=0;
}
void set_channel(int m)
{
channel=m;
cout<<"\n Current channel is"<<channel;
}
void set_volume (int n)
{
volume =n;
cout<<"\n current volume is"<<volume;
}
void channel_up()
{
channel+=1;
cout<<"\n current channel is"<<channel;
}
void channel_down()
{
channel-=1;
cout<<"\n current channel is"<<channel;
}
void vol_up()
{
volume+=1;
cout<<"\n current volume is"<<volume;
}
void vol_down()
{
volume-=1;
cout<<"\n current volume is"<<volume;
}
};
void main()
{
int x,y,z;
tv t1;
do
{
cout<<"do you want to make any changes (1/0)";
cin>>x;
if (x == 1)
{
cout<<"1. turn off \n 2.turn on \n 3. channel up \n 4. channel down \n 5.set channel \n 6.volume up \n 7.volume down \n 8.set volume \n";
cout<<"enter the number ";
cin>>y;
if (y==1)
{
t1.turn_off();
break;
}
switch (y)
{
case 2:
t1.turn_on();
break;
case 3:
t1.channel_up();
break;
case 4:
t1.channeldown();
break;
case 5:
{
cout<<"\n enter the channel no (1-120)";
cin>>z;
t1.set_channel(z);
}
break;
case 6:
t1.vol_up();
break;
case 7:
t1.vol_down();
break;
case 8:
{
cout<<"\n enter the volume level(1-7)";
cin>>z;
t1.set_volume(z);}
break;
}
}
}
while(x== 1);
cout<<"thank you";
}





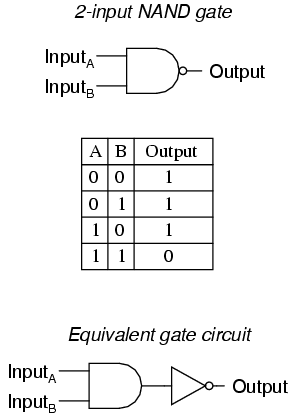

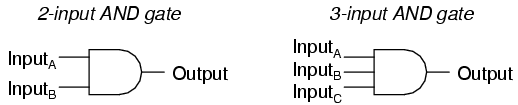



 is used between any two statements P and
Q to form a compound statement P
is used between any two statements P and
Q to form a compound statement P  is called the biconditional and may be
placed between any two statements to form a compound statement P
is called the biconditional and may be
placed between any two statements to form a compound statement P