24.06.12
Types of Compound statements and their connectives
1. A negation: formed when we negate a simple statement by "not"
Simple statement: Today is Thursday
Compound statement: negation: today is not Thursday
The sentence "today is not Thursday" is a compound statement called a negation.
2. When we connect two simple statements using "and" the result is a compound statement called a conjunction.
3. If the simple statements are joined by "or" the resulting compound statement is called a disjunction.
4. The If . . . then connector is used in compound statements called conditionals.
5. The if and only if connector is used to form compound statements called biconditionals.
We are familiar with using letters as replacements in algebra; in logic we can also use letters to replace statements. The common letters used to replace statements are P,Q, R: but any letters can be used.
For example:
P = Today is Saturday
Q = I passed my test
but P and Q would read Today is Saturday and I passed my test.
It is also common practice to use symbols for the connective words (or the connectors).
In the first column, there are two possibilities of P; P is either
True or False. Each line in the table represents a case that must be
considered. In this case, there are only two cases. The truth table
tells us the truth value of p in every case.
Truth Tables with the Connective ^Types of Compound statements and their connectives
1. A negation: formed when we negate a simple statement by "not"
Simple statement: Today is Thursday
Compound statement: negation: today is not Thursday
The sentence "today is not Thursday" is a compound statement called a negation.
2. When we connect two simple statements using "and" the result is a compound statement called a conjunction.
3. If the simple statements are joined by "or" the resulting compound statement is called a disjunction.
4. The If . . . then connector is used in compound statements called conditionals.
5. The if and only if connector is used to form compound statements called biconditionals.
We are familiar with using letters as replacements in algebra; in logic we can also use letters to replace statements. The common letters used to replace statements are P,Q, R: but any letters can be used.
For example:
P = Today is Saturday
Q = I passed my test
but P and Q would read Today is Saturday and I passed my test.
It is also common practice to use symbols for the connective words (or the connectors).
Connectors
Symbols (a) not
~ (b) and
^ (c) or
∨ (d) if . . . then
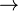
(e) if and only if 
Since a statement in logic is either true or false,
we should be able to determine the truth or falsity of a given
statement. [Logic is very precise. There should be no worry about
ambiguity] Let P be a statement; then ~ P means "not P" or the
negation of P. The negation of P is true whenever the statement P is
false and false if P is true. These situations are confusing to
write, therefore we can record these statements in a truth table.
Example:
Let P = this is a hard course.
~P= this is not a hard course.
Then this can be recorded in Truth Table as:
| P | ~P |
| T | F |
| F | T |
The Connective ^ may be placed between any two statements P and Q to form the compound statement P^Q.
Example:
Let P = Today is Monday
Q = I have a maths class
Then this can be recorded in Truth Table as:
| P | Q | P^Q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
In the compound statements, the individual statements are called
components. In a compound statement with two components such as p ^ q
there are four possibilities. These are called logical possibilities.
The possibilities are:
1) p is true and q is true
2) p is true and q is false
3) p is false and q is true
4) p is false and q is false.The four possibilities are covered in the four rows of the truth table. The last column gives values of P ^ Q; This is only true when both p and q are true. Using the examples given, truth tables of a more complicated nature can be built.
Let us consider the situation P∨Q
Example:
Let P = Today is Tuesday
Q = I have a maths class
Hence, P∨Q = Today is Tuesday or I have a maths class
Then this can be recorded in Truth Table as:
| P | Q | P∨Q |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Like ^, here are four possibilities which are covered in the four rows of the truth
table. The last column gives values of P ^ Q; This is only false when
both P and Q are false.
No comments:
Post a Comment