25.06.12
The conditional and the Biconditionals Statements.
Let P = You Passed English
Q = You will graduate
Then this can be recorded in Truth Table as:
Then this can be recorded in Truth Table as:
The conditional and the Biconditionals Statements.
If the connectors 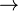 is used between any two statements P and
Q to form a compound statement P
is used between any two statements P and
Q to form a compound statement P 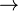 Q (reads if P then Q), the
statement is called a conditional statement.
Q (reads if P then Q), the
statement is called a conditional statement.
Example: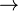 is used between any two statements P and
Q to form a compound statement P
is used between any two statements P and
Q to form a compound statement P 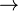 Q (reads if P then Q), the
statement is called a conditional statement.
Q (reads if P then Q), the
statement is called a conditional statement.Let P = You Passed English
Q = You will graduate
Then this can be recorded in Truth Table as:
| P | Q | P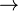 Q Q |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
The statement P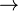 Q reads if you pass English then you will
graduate. This statement is false only when you pass English (true)
but you will not graduate. Therefore the final column will be true in
every position but the second.
Q reads if you pass English then you will
graduate. This statement is false only when you pass English (true)
but you will not graduate. Therefore the final column will be true in
every position but the second.
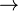 Q reads if you pass English then you will
graduate. This statement is false only when you pass English (true)
but you will not graduate. Therefore the final column will be true in
every position but the second.
Q reads if you pass English then you will
graduate. This statement is false only when you pass English (true)
but you will not graduate. Therefore the final column will be true in
every position but the second.
The connective  is called the biconditional and may be
placed between any two statements to form a compound statement P
is called the biconditional and may be
placed between any two statements to form a compound statement P  Q (reads P if and only if Q).
Q (reads P if and only if Q).
 is called the biconditional and may be
placed between any two statements to form a compound statement P
is called the biconditional and may be
placed between any two statements to form a compound statement P  Q (reads P if and only if Q).
Q (reads P if and only if Q).Then this can be recorded in Truth Table as:
| P | Q | P Q Q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
THE BINARY SYSTEM AND BOOLEAN ALGEBRA
The Boolean algebra provides rigorous
procedures for deciding whether a statement is true or false;if the
statement can be expressed in two variables. In Boolean algebra true
is represented by a 1 and false by a 0. With these two digits (0,1)
and the three basic operations called “not”, “and” and “or”,
digital algebra or switching algebra was developed.
The basic operations and their meaning:
| Operation | Meaning | Symbol |
| or | Determine a single input bit from the values of two or more input | + (A+B) |
| and | Determines a single input bit from the value of two or more input | . (A.B or AB) |
| not | Change binary bits to its opposite value | ! (!A or ~A or bar over A) |
Any relationship between logical variables are called logical
expressions. These expressions can be written as an equation for
example the equation A + B + C = F where F is the name of the output
variable. The expression A + B + C = F expresses the action of and/or
function. Through Boolean Algebra logical analysis can be performed
using these three functions.
The electronic representation of these functions are called logic
gates. There are the and gate the not and the or gates. These logic
gates are basic functional units for both arithmetic and logic
operations; to operate they must accept binary numbers, and should
have a carry bit of one or 0, (from the adjacent lower power of two),
and should produce as outputs a sum bit and a carry bit for the next
higher power of two.
The table is bit confusing please can anyone help me out to elaborate the table in a simple of the basic operations and their meaning....???
ReplyDeleteThere are 3 tables on this page, which one you want to be explained?
DeleteThe basic operations and their meaning:
ReplyDeleteOperation Meaning Symbol
or Determine a single input bit from the values of two or more input + (A+B)
and Determines a single input bit from the value of two or more input . (A.B or AB)
not Change binary bits to its opposite value ! (!A or ~A or bar over A)
this one...
This table shows working of basic operations and their meanings. These meanings can be read as A + B, this is AND which requires both inputs to generate output, A.B, this is OR which requires either input to generate output, and !A is not A or inverse of A, which is NOT gate.
Delete